多臂老虎机

一、多臂老虎机问题

假设在一家赌场有多台老虎机，每台机器拉一下手柄都会随机给出一定的金币作为奖励，但不同机器的回报率各不相同且事先未知。怎样在有限的尝试次数内，尽可能多地赢取金币，就是经典的 多臂老虎机（Multi‐armed Bandit, MAB）问题。

多臂老虎机的玩家既要“探索”未知臂以便发现更高的期望收益，也要“利用”目前已知的优臂以获取更多回报。所以多臂老虎机问题的核心在于：如何 在探索和利用之间做出最优平衡（exploration–exploitation trade-off），以最大化累积回报或最小化累积遗憾。

（一）数学建模

设有 $K$ 个臂，每个臂 $i$ 对应一个未知概率分布 $P_i$，奖励取值范围设为 $[0,1]$（可以归一化），记：

• $X_{i,t} \sim P_i$：第 $t$ 次选择臂 $i$ 获得的奖励；
• $\mu_i = \mathbb{E}[X_{i,t}]$：臂 $i$ 的期望奖励（固定但未知）；
• $\mu^* = \max_{1 \le i \le K} \mu_i$：最优臂的期望奖励；
• $A_t$：第 $t$ 轮选择的臂编号；
• $T$：总轮数（时间步数）；

目标是设计策略 $\pi$ 来最小化 累积遗憾（Cumulative Regret）：

$$Rt(T) = T\mu^* - \mathbb{E} \left[\sum_{t=1}^T X_{A_t,t} \right] = \sum_{i=1}^T \Delta_i \cdot \mathbb{E}[N_i(T)] \quad \text{(越小越好)}$$

其中：

• $\Delta_i = \mu^* - \mu_i$ 是臂 $i$ 的“劣势”；
• $N_i(T) = \sum_{t=1}^T \mathbb{I}\{A_t = i\}$ 是臂 $i$ 被选择的次数；

这个遗憾函数反映了我们策略由于没有总是选择最优臂而损失的期望奖励。

由于 $T\mu^{\ast}$ 是个固定值，最小化累计遗憾也等价于最大化 累计奖励（Cumulative Reward）：

$$Rd(T) = \mathbb{E}\left[\sum_{t=1}^T X_{A_t,t}\right] \quad \text{(越大越好)}$$

（二）求解算法

1. $\varepsilon$- 贪心算法（$\varepsilon$-Greedy）

设 $\hat{\mu}_i(t)$ 为到第 $t$ 轮为止臂 $i$ 的平均奖励估计：

$$\hat{\mu}_i(t) = \frac{1}{N_i(t)} \sum_{s=1}^{t} X_{i,s} \cdot \mathbb{I}\{A_s = i\}$$

其中：

• $N_i(t)$：到第 $t$ 轮为止臂 $i$ 被选择的次数；
• $X_{i,s}$：第 $s$ 轮从臂 $i$ 获得的奖励；
• $\mathbb{I}\{A_s = i\}$ 是指示函数，表示第 $s$ 轮是否选择了臂 $i$。

$\varepsilon$-Greedy 算法是求解 MAB 问题最简单的策略：

• 以概率 $1 - \varepsilon$ 选择当前平均奖励最高的臂（利用）；
• 以概率 $\varepsilon$ 随机选择一个臂（探索）。

$\varepsilon$-Greedy 算法的缺点为：固定的 $\varepsilon$ 会导致 线性遗憾。随着时间推移，臂的奖励大小会越来越明确，此时应该以利用为主，减少无谓探索。固定的 $\varepsilon$ 会始终浪费一定时间进程试错，即策略中“乱选”的部分不会随着学习而减少。

$\varepsilon$-Greedy 算法的改进方法为：随时间减小 $\varepsilon$，例如设置：

$$\varepsilon_t = \frac{1}{t} \quad \text{或} \quad \varepsilon_t = \frac{1}{\sqrt{t}}$$

这表示初期我们多探索（$\varepsilon_t$ 较大）；随着时间增长，我们更倾向于利用已知信息（$\varepsilon_t$ 趋近于 0）；这样策略越来越稳定，最终能逼近最优臂，获得 次线性遗憾。

2. 上置信界算法（UCB1）

UCB1 的核心思想是：利用置信区间（confidence bound）做乐观估计，优先尝试“可能好”的臂。

UCB1 通过计算 当前平均奖励 + 一个鼓励探索的项（不确定性） 来估计每个臂的乐观表现，并挑选最乐观的臂：

$$A_t = \arg\max_{1 \le i \le K} \left(\hat{\mu}_i(t-1) + \sqrt{\frac{2 \ln t}{N_i(t-1)} } \right)$$

其中：

• $\hat{\mu}_i(t-1)$：第 $t-1$ 步时臂 $i$ 的平均奖励；
• $N_i(t-1)$：到 $t-1$ 步为止，臂 $i$ 被选择的次数，臂被选中的次数越多，臂的奖励的不确定性越小，探索项越小；
• $\sqrt{\frac{2 \ln t}{N_i(t-1)} }$ 是 置信区间的宽度，衡量不确定性，它是根据 Hoeffding 不等式推导而来：

Hoeffding 不等式 ：假设有 $n$ 个独立的、取值范围在 $[0,1]$ 的随机变量，那么它们的平均值 $\hat{\mu}$ 与真实期望 $\mu$ 的偏差是有 上界 的：

$$\Pr\left(|\hat{\mu} - \mu| \ge \epsilon \right) \le 2 \exp(-2n \epsilon^2)$$

我们想找一个 置信区间宽度 $\epsilon(n)$，使得真实期望 $\mu$ 落在以下区间的概率很高：

$$\Pr\left(\mu \le \hat{\mu} + \epsilon(n) \right) \ge 1 - \delta$$

等价地：

$$\Pr\left(\hat{\mu} + \epsilon(n) <\mu \right) \le \delta$$

根据 Hoeffding 不等式，我们只要让偏差上界等于 $\delta$：

$$\exp(-2n \epsilon^2) = \delta \quad\Rightarrow\quad \epsilon = \sqrt{\frac{ \ln(1/\delta) }{2n} }$$

UCB1 并不使用固定的置信水平 $\delta$，而是设置：

$$\delta = \frac{1}{t^4} \quad\Rightarrow\quad \ln \left(\frac{1}{\delta} \right) = 4 \ln t$$

这时置信区间变成：

$$\epsilon = \sqrt{\frac{4 \ln t}{2n} } = \sqrt{\frac{2 \ln t}{n} }$$

代入 $n = N_i(t-1)$，就得到了 UCB1 中使用的 探索项（置信区间宽度）：

$$\epsilon = \sqrt{\frac{2 \ln t}{N_i(t-1)} }$$

UCB1 算法保证了前期探索，后期利用的整体策略，且累积遗憾是次线性的。UCB1 算法有严谨的上界分析，理论性能优秀。

3. 汤普森采样（Thompson Sampling）

汤普森采样（Thompson Sampling）也称为概率匹配法（Probability Matching），其核心思想是利用贝叶斯推理，挑选最大化后验概率分布期望的动作。

贝叶斯推理 是统计学中基于贝叶斯定理的概率更新方法，其核心思想是通过新证据（数据）动态修正对未知参数的先验认知。

贝叶斯定理 的数学表达如下：

$$P(\theta \mid \text{data}) = \frac{P(\text{data} \mid \theta) \cdot P(\theta)}{P(\text{data})}$$

其中：

• $P(\theta)$：先验分布（Prior），表示在观测数据前对参数 $\theta$ 的初始认知（如历史经验或主观假设）。
• $P(\text{data} \mid \theta)$：似然函数（Likelihood），描述在给定 $\theta$ 时，当前数据出现的概率。
• $P(\theta \mid \text{data})$：后验分布（Posterior），整合数据后对 $\theta$ 的更新认知。
• $P(\text{data})$：观测数据，即 证据（Evidence），作为归一化常数，确保后验积分为 1。

在贝叶斯统计中，如果后验分布与先验分布属于同一类分布族，则它们被称为 共轭分布。

使用汤普森采样求解 MAB 问题时，通常采用如下 设定：

1. 臂的奖励分布（似然分布）为伯努利分布

   • 每个臂 $i$ （$i=1,\dots,K$）的真实未知成功概率记为 $p_i$。

   • 每次拉动臂 $i$ 会得到一个二值奖励：

     $$X_{i,t} \sim \mathrm{Bernoulli}(p_i),\quad X_{i,t} \in \{0,1\},\quad \Pr[X_{i,t}=1] = p_i, \Pr[X_{i,t}=0] = 1-p_i.$$

2. 奖励分布中的参数分布（先验分布）为 Beta 分布

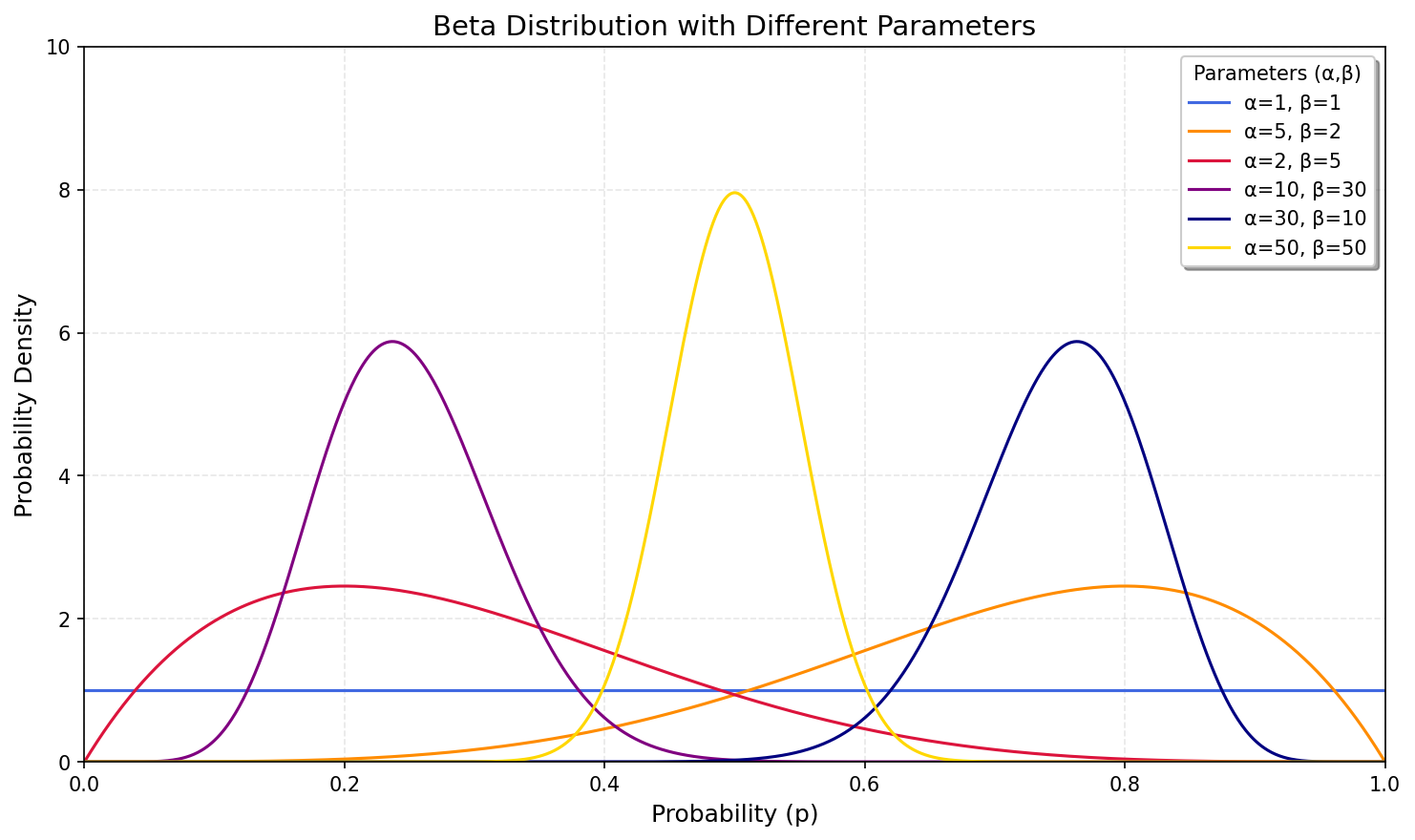
   • 设定成功概率 $p_i$ 的先验分布为 Beta 分布：

   • 通常若没有任何先验信息，可以取 $\alpha_i=\beta_i=1$，即 $\mathrm{Beta}(1,1)$（等价于 $p_i$ 为均匀分布）

     $$p_i \sim \mathrm{Beta}(\alpha_i, \beta_i)$$

3. 根据贝叶斯统计的共轭性，后验分布也为 Beta 分布

   • 设每次对臂 $i$ 做一次拉动、观察到“成功”（奖励 $=1$）或“失败”（奖励 $=0$）后，都要更新对 $p_i$ 的后验分布。
   • 假设到第 $t-1$ 轮为止，臂 $i$ 已被拉了 $S_i$ 次成功、$F_i$ 次失败（注意：这里 $S_i + F_i = N_i(t-1)$，即被选次数）。

   • 如果先验 $p_i\sim\mathrm{Beta}(\alpha_i,\beta_i)$，且观测到 $S_i$ 次成功、$F_i$ 次失败，那么 $p_i$ 的后验分布依旧是一个 Beta 分布：

     $$p_i \bigg| \{X_{i,s}\}_{s=1}^{t-1} \sim \mathrm{Beta}(\alpha_i + S_i,\beta_i + F_i)$$

   • 换句话说，到第 $t-1$ 轮时，臂 $i$ 的后验分布参数为：

     $$\alpha_i(t-1) = \alpha_i(0) + S_i, \quad\beta_i(t-1) = \beta_i(0) + F_i$$

根据汤普森采样， 第 $t$ 轮挑选臂的 策略 为：

1. 对每个臂 $i$ 从其后验分布中随机抽一个样本：

   $$\theta_i \sim \mathrm{Beta}\bigl(\alpha_i(t-1),\beta_i(t-1)\bigr)$$

   这里 $\theta_i$ 可以看作“根据到目前为止的信息，臂 $i$ 的潜在真实成功率”的一个随机猜测。

2. 根据抽样值 $\{\theta_i\}_{i=1}^K$ 选臂：

   $$A_t = \arg\max_{1 \le i \le K} \bigl\{\theta_i\bigr\}$$

   换句话说，实际选择那个“这次恰好随机抽得最大 $\theta_i$”的臂。

3. 拉动所选臂 $A_t$，观察到奖励 $X_{A_t,t} \in \{0,1\}$。

   • 若 $X_{A_t,t} = 1$，说明成功一次，于是更新该臂的 “成功计数” $S_{A_t} \leftarrow S_{A_t} + 1$，对应后验参数 $\alpha_{A_t} \leftarrow \alpha_{A_t} + 1$。
   • 若 $X_{A_t,t} = 0$，说明失败一次，于是更新该臂的 “失败计数” $F_{A_t} \leftarrow F_{A_t} + 1$，对应后验参数 $\beta_{A_t} \leftarrow \beta_{A_t} + 1$。
4. 重复上述步骤到第 $T$ 轮结束。

随着轮次 $t$ 的增加，我们不断更新后验分布，每个臂 $i$ 的后验分布 $\mathrm{Beta}(\alpha_i(t-1),\beta_i(t-1))$ 越来越集中，其均值 $\frac{\alpha_i(t-1)}{\alpha_i(t-1) + \beta_i(t-1)}$ 也会越来越接近真实值 $p_i$ 。这时越有可能是最优的臂，它被抽到的概率就越大，充分利用了已有信息；但同时由于不确定性，偶尔也会有次优但尚未充分探索的臂被选到，以此积累更多信息。

汤普森采样从贝叶斯视角自然地平衡探索与利用，累积遗憾是次线性的，在实践中表现往往优于 UCB1，且可以扩展到非伯努利奖励、多维上下文等更复杂的场景。

二、多臂老虎机变体问题

（一）上下文 MAB（Contextual Bandits）

每一轮决策前都会收到一个上下文（context）向量 $x_t \in \mathbb{R}^d$，它描述了当前时刻的环境信息。奖励不仅取决于选择的臂，还与上下文相关。

目标是设计一个策略 $\pi(x_t)$，使得在上下文 $x_t$ 出现时选臂 $A_t = \pi(x_t)$，从而最大化累计期望奖励 $\sum_{t=1}^T \mathbb{E}[X_{A_t,t}]$。

1. LinUCB 算法

假设与上下文相关的奖励服从线性回归模型：

$$\mathbb{E}\bigl[X_{i,t} \bigm| x_t\bigr] = x_t^\top \theta_i$$

其中，$\theta_i \in \mathbb{R}^d$ 是臂 $i$ 的未知参数向量，用来衡量在不同上下文下，臂 $i$ 的期望奖励。

LinUCB 假设对每个臂 $i$ 都做一个带正则化的线性回归，用历史数据来估计 $\theta_i$。具体步骤如下：

1. 维护矩阵和向量
   对臂 $i$，设它从开始到目前被选过 $n_i$ 次，所对应的上下文矩阵为：

   $$D_i = \begin{bmatrix} x_{i,1}^\top \\ x_{i,2}^\top \\ \vdots \\ x_{i,n_i}^\top \end{bmatrix} \in\mathbb{R}^{n_i \times d}$$

   其中第 $j$ 行 $x_{i,j}^\top$ 就是第 $j$ 次选了臂 $i$ 时的上下文。
   同时，把对应的历史奖励（随机变量）记作向量：

   $$Y_i = \begin{bmatrix} X_{i,1} \\ X_{i,2} \\ \vdots \\ X_{i,n_i} \end{bmatrix} \in\mathbb{R}^{n_i}$$

2. 构造协方差矩阵 $A_i$ 和估计 $\hat{\theta}_i$
   引入正则化系数 $\lambda > 0$，定义：

   $$A_i = D_i^\top D_i + \lambda I_d$$

   这其中 $D_i^\top D_i$ 是普通最小二乘所用的 “Gram 矩阵”，$\lambda I_d$ 用来保证可逆并防止过拟合。
   $\theta_i$ 对应的回归估计为：

   $$\hat{\theta}_i = A_i^{-1}D_i^ \top Y_i$$

   那么在第 $t$ 轮到来且上下文为 $x_t$ 时，臂 $i$ 的奖励估计就是 $x_t^\top \hat{\theta}_i$。

3. 计算上置信界并选择臂
   LinUCB 会为每个臂 $i$ 计算一个上置信界（Upper Confidence Bound）：

   $$\text{UCB}_i(t) = x_t^\top \hat{\theta}_i + \alpha \sqrt{x_t^\top A_i^{-1} x_t},$$

   这里：

   • $x_t^\top \hat{\theta}_i$ 就是“基于回归模型的当前估计均值”（利用）；
   • $\sqrt{x_t^\top A_i^{-1} x_t}$ 表示“在这个 $x_t$ 方向上的估计不确定度”（探索），如果臂 $i$ 过去在相似上下文下数据不够，$A_i^{-1}$ 在对应方向就比较大。乘上调节系数 $\alpha$（一般取稍大，比如 1 或 2），可以给不确定的臂更多探索的空间。

   最终选择“奖励估计 + 探索补偿”最大的臂为最优臂：

   $$A_t = \arg\max_{1 \le i \le K}\Bigl\{x_t^\top \hat{\theta}_i + \alpha\sqrt{x_t^\top A_i^{-1} x_t}\Bigr\}$$

4. 观测奖励并更新
   选到臂 $A_t$ 后，拉动它得到真实奖励 $X_{A_t,t}$，再把这一对 $\bigl(x_t, X_{A_t,t}\bigr)$ 加入对应的 $(D_{A_t}, Y_{A_t})$ 中，更新：

   $$D_{A_t} \leftarrow \begin{bmatrix} D_{A_t} \\[4pt] x_t^\top \end{bmatrix},\qquad Y_{A_t} \leftarrow \begin{bmatrix} Y_{A_t} \\[4pt] X_{A_t,t} \end{bmatrix},$$

   然后重新计算：

   $$A_{A_t} = D_{A_t}^\top D_{A_t} + \lambda I,\quad \hat{\theta}_{A_t} = A_{A_t}^{-1} D_{A_t}^\top Y_{A_t}.$$

   这样下一轮到来时，模型对臂 $A_t$ 的 $\theta_{A_t}$ 估计就会更准确。

（二）非平稳 MAB（Non-Stationary Bandits）

在经典 MAB 中，我们假设每个臂 $i$ 的期望奖励 $\mu_i$ 是固定不变的。但在很多实际场景下（比如用户偏好随时间变化、设备老化导致性能波动等），臂的真实期望 $\mu_i(t)$ 会随着时间 $t$ 改变。这时如果继续用固定环境下的算法，往往会把过去积累的大量“旧数据”当作对当前环境的有效信息，而没有及时跟“新现象”对齐，决策出现严重劣化。

非平稳 MAB 的核心需求就是：策略能够适应这类“随时间漂移”的奖励分布，对古老数据加以“遗忘”或“衰减”，让自己的决策更多依赖于最近的观察。

• $X_{i,t}$：第 $t$ 轮拉臂 $i$ 时得到的随机奖励。
• $A_t$：第 $t$ 轮选中的臂编号。
• $\hat{\mu}_i(t)$：针对臂 $i$ 在第 $t$ 轮的当前平均奖励估计。

1. 滑动窗口 UCB（SW-UCB）

思路：只用最近 $w$ 轮得到的数据来估计每个臂的当前平均和置信区间，舍弃更早数据。这样可以在环境突变时快速“忘掉”过时信息。

1. 窗口内次数统计
   定义滑动窗口（最近 $w$ 轮的索引集合）：

   $$\mathcal{W}_t = \{s : t - w + 1 \le s \le t\}$$

   对臂 $i$ 而言，记在窗口 $\mathcal{W}_t$ 中被选择的总次数为：

   $$N_i^{\mathrm{win}}(t) = \sum_{s = t - w + 1}^{t} \mathbb{I}\{A_s = i\}$$

2. 滑动窗口内平均奖励
   在第 $t$ 轮，要估计臂 $i$ 的当前平均奖励，只使用最近 $w$ 轮拉该臂时观察到的奖励：

   $$\hat{\mu}_i(t) = \begin{cases} \displaystyle \frac{1}{N_i^{\mathrm{win}}(t)} \sum_{s = t - w + 1}^{t} X_{i,s} \mathbb{I}\{A_s = i\}, & N_i^{\mathrm{win}}(t) > 0, \\[8pt] 0, & N_i^{\mathrm{win}}(t) = 0, \end{cases}$$

   其中若 $N_i^{\mathrm{win}}(t)=0$ 表示在窗口期内尚未拉过臂 $i$，可先将 $\hat{\mu}_i(t)$ 设为 0 或者一个默认值，以保证算法会去探索它一次。

3. 滑动窗口 UCB
   类似常规 UCB，只不过“奖励估计 + 置信区间”都限制在窗口内数据：

   $$\mathrm{SW\text{-}UCB}_i(t) = \hat{\mu}_i(t) + c \sqrt{\frac{\ln t}{N_i^{\mathrm{win}}(t)}}$$

   其中：

   • $\displaystyle \sqrt{\frac{\ln t}{N_i^{\mathrm{win}}(t)}}$ 是基于窗口内样本数的置信宽度；
   • 常数 $c>0$ 用来调节探索强度；
   • 如果在窗口内 $N_i^{\mathrm{win}}(t)=0$（尚无样本），通常将该臂的 UCB 视为 $+\infty$，以保证它至少被试一次。

4. 选择与更新
   第 $t$ 轮到来时，先计算每个臂的 $\mathrm{SW\text{-}UCB}_i(t)$，然后选择：

   $$A_t = \arg\max_{1\le i\le K}\mathrm{SW\text{-}UCB}_i(t)$$

   拉臂 $A_t$，观测奖励 $X_{A_t,t}$ 并存入时间戳 $t$；
   下一轮 $t+1$ 到来时，窗口滑动为 $\{t - w + 2, \dots, t+1\}$，重新统计新的 $N_i^{\mathrm{win}}(t+1)$ 和 $\hat{\mu}_i(t+1)$，如此循环。

通过只看最近 $w$ 轮的数据，SW-UCB 能够丢弃旧分布的统计，快速适应新分布。但窗口大小 $w$ 的选取非常重要：窗口太小，数据不够，估计方差大；窗口太大，忘却慢，适应性差。

2. 指数加权平均（EXP3.S）

思路：给每个臂维护一个权重，用它来计算各臂的概率分布；每轮得到的奖励不仅立即用于更新，还会被“指数衰减”以快速忘却旧数据。

1. 初始化
   对每个臂 $i=1,\dots,K$，初始化一个权重 $w_i(1) = 1$。
   设定衰减因子 $\rho \in (0,1)$（如 $0.99$），学习率 $\eta > 0$，探索参数 $\gamma \in (0,1)$。

2. 每轮计算概率
   在第 $t$ 轮，根据当前权重计算选臂概率向量 $\{p_i(t)\}$：

   $$p_i(t) = (1 - \gamma)\frac{w_i(t)}{\sum_{j=1}^K w_j(t)} + \frac{\gamma}{K}, \quad i = 1,\dots,K$$

   其中 $\frac{w_i(t)}{\sum_j w_j(t)}$ 是“利用”部分，让高权重臂被选概率大；$\gamma/K$ 保证全局随机“探索”。

3. 抽样与拉臂
   按 $\{p_i(t)\}$ 的概率分布随机选择一个臂 $A_t$，拉一次并观测奖励 $X_{A_t,t}$。

4. 权重的指数更新（带衰减）
   首先，对臂 $i$ 构造加权奖励估计：

   $$\widehat{X}_{i,t} = \begin{cases} \displaystyle \frac{X_{i,t}}{p_i(t)}, & \text{if} i = A_t, \\[8pt] 0, & \text{if} i \neq A_t. \end{cases}$$

   然后，对所有臂先做“指数衰减”：

   $$w_i(t) \longleftarrow \rho w_i(t), \quad i=1,\dots,K$$

   再针对被选臂 $A_t$ 用当前的“加权奖励” $\widehat{X}_{A_t,t}$ 做指数更新：

   $$w_{A_t}(t+1) = w_{A_t}(t) \exp\Bigl(\eta \widehat{X}_{A_t,t}\Bigr)$$

   其余 $i \neq A_t$ 的权重在仅做“衰减”后，直接形成下一轮权重：

   $$w_i(t+1) = w_i(t), \quad i \neq A_t$$
5. 第 $(t+1)$ 轮继续
   更新后权重 $\{w_i(t+1)\}$，下一轮按照相同步骤计算新的 $\{p_i(t+1)\}$，继续抽样拉臂。

EXP3.S 通过“指数衰减”快速遗忘旧数据，又通过“指数增益”放大近期表现好的臂，能够在非平稳或对抗环境下迅速调整，保持算法对最新变化的敏感性。